Covariance is a statistical measure of the extent that 2 variables move in tandem relative to their respective mean (or average) values.
In the investment world, it is important to be able to measure how different financial variables interact together.
Covariance can provide clues to the following two questions:
- Are there common factors affecting the returns of your investments?
- How can you measure the magnitude of this relationship?
It is calculated by taking the product of two variables’ deviations from their average values.
The practical applications of covariance are quite significant in statistics, economics, finance, and portfolio management.
Investment decision-making based on covariance analysis can have serious financial implications, and as such, it is important to be well-grounded in its understanding.
Formula of Covariance
Quite often, covariance analysis aims to assess historical relationships among variables of interest.
If we obtain a sample of monthly returns for two stocks, X and Y, covariance can be calculated as:
Where,
Xi = return (%) for stock X for period i
Yi = return (%) for stock Y for period i
X = sample mean or average value of X for sample n
Y = sample mean or average value of Y for sample b
n = sample size (12 observation implies n=12)
Note: the formula above is the covariance computation for a sample of data. When working with a population (the entire data), the denominator changes to (n) rather than (n-1).
Example Calculations
Assume we want to compute the covariance of a sample of monthly returns (%) for stock X and stock Y for 2010. The following table summarizes the return data, as well as all necessary calculations for both stocks:
| Stock X Returns (%) | Stock Y Returns (%) | ||||
| Date | (%) | (%) | |||
| Jan-10 | 1.80 | 1.25 | 0.86 | -0.59 | -0.51 |
| Feb-10 | 2.20 | 2.65 | 1.26 | 0.81 | 1.02 |
| Mar-10 | 0.80 | 1.36 | -0.14 | -0.48 | 0.07 |
| Apr-10 | -1.50 | -2.36 | -2.44 | -4.20 | 10.26 |
| May-10 | 1.75 | 2.95 | 0.81 | 1.11 | 0.90 |
| Jun-10 | -3.65 | 1.78 | -4.59 | -0.06 | 0.29 |
| Jul-10 | 4.75 | 1.85 | 3.81 | 0.01 | 0.02 |
| Aug-10 | 1.30 | 2.9 | 0.36 | 1.06 | 0.38 |
| Sep-10 | -2.15 | 3.5 | -3.09 | 1.66 | -5.12 |
| Oct-10 | 3.75 | 2.6 | 2.81 | 0.76 | 2.12 |
| Nov-10 | 1.95 | 2.15 | 1.01 | 0.31 | 0.31 |
| Dec-10 | 0.25 | 1.5 | -0.69 | -0.34 | 0.24 |
| Mean Value = | 0.94 | 1.84 | Sum = | 9.98 |
We calculate covariance using the formula above:
Therefore, there is a positive relationship between the returns of Stock X and Stock Y. In other word, the returns of both stocks tend to move in the same direction for the sample of interest
Limitations of Covariance
The major limitation of the covariance measure is in its interpretation. While we can gauge the directional relationship between the variables, the magnitude in itself, is not very informative. From the above example, a covariance of 0.91 does not tell us how strong the relationship between the returns of Stock X and Y is, and as such, our conclusions are limited. One way we can work around this shortcoming is to determine the correlation coefficient.
Another short-coming in covariance is that the result is highly sensitive to the volatility of the variables’ variances. For example, the presence of just a few outliers in a data set can significantly skew its result, rendering it as a potentially misleading statistic, in terms if interpretation.
Covariance in Portfolio Management Theory
Portfolio management theory (or Modern Portfolio Theory (MPT)), as developed by Harry Markowitz in the 1950s, makes extensive use of the covariance measure. The theory posits that an efficient frontier exists, which is derived from the expected returns and variances (or standard deviation) of sets of investment portfolios. Given varying weights in two asset classes (e.g. stocks and bonds), we can determine risk-efficient points on a graph plotting the expected returns and standard deviations of the portfolio. The line of the graph is the efficient frontier. In other words, the EF plots the maximum return possible given a level of risk (variance).
The role of covariance in MPT lies in its impact on the diversification effects of adding an individual investment, portfolio, or different asset class to an existing portfolio. Thus, given an existing portfolio, it is possible to reduce its inherent risk (for a given expected return) by adding an investment whose returns exhibits a low covariance with those of the existing portfolio.
Conclusion
Covariance is a statistical measure of the extent and direction of co-movement between two variables deviations from their respective means. It can be used to assess the association between important economic and financial data such as stock returns, equity indexes, bond returns, inflation, interest rates, and a multitude of relationships of interest. Covariance analysis can also be used to assess the diversification benefits of adding different asset classes into our portfolio. Its limitation is the difficultly in its interpretation, since the strength of the relationship cannot be strongly gauged from its result.

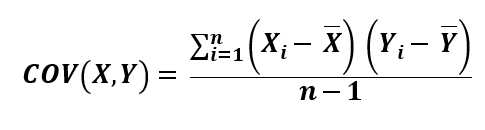
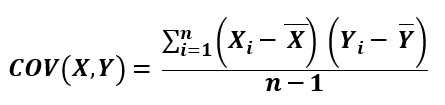
 Diversification
Diversification